図形と計量
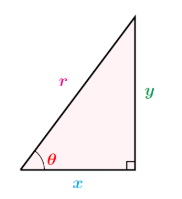
三角比
正弦 : $sin\theta=\frac{y}{r}$
余弦 : $cos\theta=\frac{x}{r}$
正接 : $tan\theta=\frac{y}{x}$
三角比の相互関係
- $tan\theta=\frac{sin\theta}{cos\theta}$
- $sin^2\theta+cos^2\theta=1$
- $1+tan^2\theta=\frac{1}{cos^2\theta}$
90°-θ
- $sin(90°-\theta)=cos\theta$
- $cos(90°-\theta)=sin\theta$
- $tan(90°-\theta)=\frac{1}{tan\theta}$
180°-θ
- $sin(180°-\theta)=sin\theta$
- $cos(180°-\theta)=-cos\theta$
- $tan(180°-\theta)=-tan\theta$
y=mxとx軸の正の向きとなす角をθとする
m=tanθ
応用
正弦定理 △ABCの外接円の半径をRとすると $\frac{a}{sinA}=\frac{B}{sinB}=\frac{c}{sinC}=2R$
余弦定理
△ABC
$a^2=b^2+c^2-2bccosA$
$b^2=c^2+a^2-2cacosB$
$c^2=a^2+b^2-2abcosC$
$cosA=\frac{b^2+c^2-a^2}{2bc}$
$cosB=\frac{c^2+a^2-b^2}{2ca}$
$cosC=\frac{a^2+b^2-c^2}{2ab}$
三角形の2辺の大小関係はその向かい合う角の大小関係と一致する。
面積
△ABCの面積をSとすると
$S=\frac{1}{2}bcsinA=\frac{1}{2}casinB=\frac{1}{2}absinC$
内接円 : 三角形の3辺に接する円
三角形の内接円と面積
$S=\frac{1}{2}r(a+b+c)$
ヘロンの公式
$S=\sqrt{s(s-a)(s-b)(s-c)},s=\frac{a+b+c}{2}$
MEMO
黄金比 : 1+$\frac{1+\sqrt{5}}{2}$